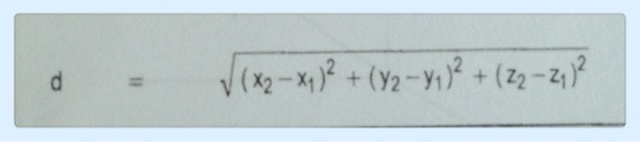1.1 พิกัดฉากในปริภูมิสามมิติ
ระบบแกนพิกัดฉากในปริภูมิสามมิติ เป็นระบบที่ประกอบด้วยเส้นตรงสามเส้นตั้งฉากซึ่งกันและกัน ตัดกันที่จุดกำเนิด 0 เส้นตรงทั้งสามเรียกว่า แกน x แกน y แกน z ดังรูปที่ 1.1
รูปที่ 1.1
แกนพิกัดแต่ละคู่เป็นตัวกำหนดระนาบซึ่งเรียกว่า ระนาบพิกัด ประกอบด้วย ระนาบ xy ระนาบ xz ระนาบ yz ดังนั้นปริภูมิจะแบ่งออกเป็น 8 ส่วน ดั้งรูปที่ 1.2
จุดในปริภูมิสามมิติ จะถูกกำหนดโดยจำนวน 3 จำนวน ถ้าเราให้ P เป็นจุดในปริภูมิสามมิติ มีแกนพิกัดฉากเป็นที่อ้างอิง แทน P ด้วยจำนวน 3 จำนวนในที่นี้แทนด้วย (a,b,c) พิกัดของจุด P ก็คือ (a,b,c) เราเขียนแทนด้วย P (a,b,c) เป็นจุดที่เกิดจากระนาบ 3ระนาบ ผ่านจุด P และขนานกับระนาบพิกัด โดยมี a,b และ c เป็นพิกัดของการตัดกันของระนาบนี้กับแกน x,y และ z ตามลำดับ ดังรูป 1.3
รูปที่ 1.3
1.2 ระยะทางคะหว่างจุด 2 จุด ในปริภูมิสามมิติ
นิยาม 1.1 กำหนดให้ P1 (x1,y1,z1) และ P2 (x2,y2,z2) เป็นจุด 2จุด ในปริภูมิมิติ และให้ d เป็นระยะทางระหว่างจุด P1 และ P2 แล้วจะได้ว่า
สำหรับจุด P,Q,R ในปริภูมิสามมิตินั้น มีข้อสังเกตดังนี้
1. ระยะทางระหว่าง P และ Q มากกว่าหรือเท่ากับศูนย์ และระยะทางเป็นศูนย์ก็ต่อเมื่อ P เป็นจุดเดียวกันกับ Q
2. ระยะทางระหว่าง P และ R น้อยกว่าหรือเท่ากับ ผลบวกของระยะทางระหว่าง P และ Q และ ระยะทางระหว่าง Q และ R
1.3 เวกเตอร์ในปริภูมิสามมิติ
จากที่กล่าวมาไว้ในตอนต้นแล้วว่าเวกเตอร์เป็นปริมาณที่มีขนาดและทิศทาง ดังนั้นสิ่งที่ใช้แทนเวกเตอร์จึงต้องเป็นสิ่งที่สามารถแสดงได้ทั้งสองอย่าง ในที่นี้เราจะให้ส่วนของเส้นตรงที่เชื่อมโยงระหว่างจุด 2 จุด และมีหัวลูกศรกำกับแทนเวกเตอร์ ให้ความยาวของส่วนของเส้นตรงแทนขนาดและหัวลูกศรบอกทิศทาง เรียกส่วนของเส้นตรงนี้ว่า ส่วนของเส้นตรงที่มีทิศทาง
นิยาม 1.2 ถ้า